¶ Datenstrukturen und Algorithmen
Programmiersprachen setzen verschiedene Programmierparadigmen um.
Zur Wiederholung aus den letzten Jahren
¶ primitive Datentypen
In Python stehen verschiedene Datentypen zur Verfügung.

| Datentyp | Beschreibung | Beispiel |
|---|---|---|
| Integer | Ganzzahl | 4,1,-7 |
| Float | Kommazahl | 3.14, 5.55, -6.1 |
| Boolean | Wahrheitswert | True, False, 1 != 0, 0 == 5, 1 < 7 |
| String | Zeichenkette | "Hallo Welt!" |
| List | Liste | ["Eier", "Milch", "Zucker"], [1, 5, 7, 9, 3], [True, False, False] |
¶ komplexe Datenstrukturen
Eine Datenstruktur ist ein Objekt, welches zur Speicherung und Organisation von Daten dient. Es handelt sich um eine Struktur, weil die Daten in einer bestimmten Art und Weise angeordnet und verknüpft werden, um den Zugriff auf sie und ihre Verwaltung effizient zu ermöglichen.
Datenstrukturen sind nicht nur durch die enthaltenen Daten charakterisiert, sondern vor allem durch die Operationen auf diesen Daten, die Zugriff und Verwaltung ermöglichen und realisieren.
Quelle: https://de.wikipedia.org/wiki/Datenstruktur
Folgende Datenstrukturen werden wir betrachten.
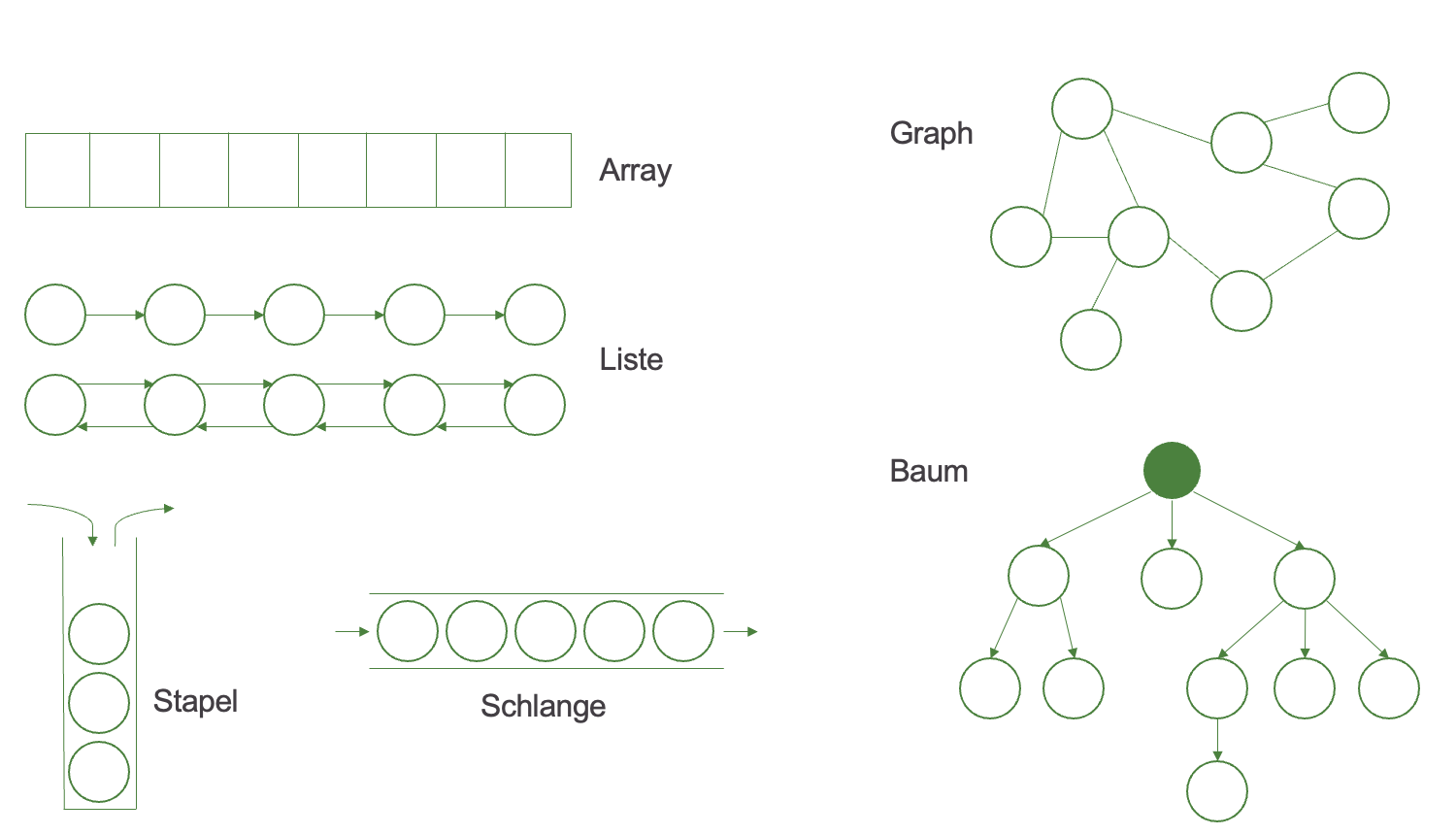
¶ Liste vs. Array
Listen und Arrays bieten die Möglichkeit, mehrere Objekte zu speichern. Sie der Aufbau dieser Strukturen unterscheidet sich stark. Die oberste Abbildung zeigt ein Array, die weiteren Listen (einfach verkettet und doppelt verkettet).

¶ Im Vergleich:
| Liste | Array | |
|---|---|---|
| Datentyp Elemente | unterschiedlich | gleich (da gleiche Größe notwendig) |
| Nutzbarkeit in Python | direkt nutzbar (l = [1,2,3]) | extra Import notwendig |
| Verwendung | kleineren Mengen an Elementen | größeren Mengenn an Elementen |
| Änderungen (Hinzufügen, Löschen und Aktualisieren) | einfach | schwierig |
| Speicherplatzbedarf | viel, da Zusatzinformationen (next) notwendig | wenig, da nur Datenelement gespeichert |
¶ Komplexität von Operationen auf Liste / Array
| Operation | Array | Linked List |
|---|---|---|
| Zugriff auf das n-te Element: | O(1) | O(n) |
| Einfügen eines Elements: | O(n) | O(1) |
| Entfernen eines Elements: | O(n) | O(1) |
| Bestimmung der Länge: | O(1) | O(n) |
¶ Datenstruktur Liste
Wie in der Abbildung oben ersichtlich, existieren verschiedene Möglichkeiten, Listen zu implementieren. Alle Listen sollten aber die gleichen Methoden anbieten. Diese können in einer Elternklasse angelegt werden. Die Implementierung erfolgt in den abgeleiteten Klassen.
Hier das Klassendiagramm unser einfach verketteten Liste aus dem Unterricht. Das UML-Diagramm enthält bereits die Vererbung. Die Implementierung noch nicht.
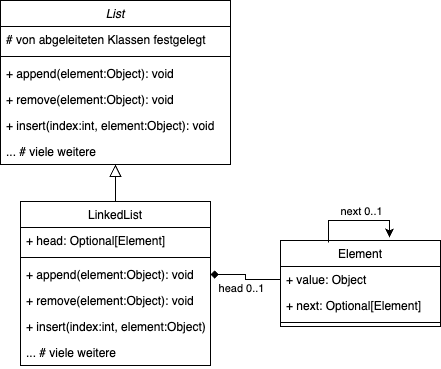
Erweitert das UML-Klassendiagram um die Klasse DoubleLinkedList für eine doppelt verkettete Liste.
Listen bieten viele Methoden an. Die folgende Tabelle zeigt einige. (Hinweis: die Namen sind teils länger als üblich, dies soll hier dem Verständnis dienen. Optional[Datentyp] bedeute, dass der Rückgabewert entweder ein Objekt vom gegebenen Typ ist, oder nichts (also void/None)).
| Methode | Hinweis |
|---|---|
| +contains(value:object):boolean | True, wenn der value in der Liste enthalten ist, sonst False |
| +clear(): void | löscht alle Elemente (setzt einfach den head der Liste auf None) |
| +get_value_at_index(index:int):Optional[Object] | gibt den Wert am Index zurück, oder None, wenn der Index nicht existiert. |
| +get_index_of_element(value:object):int | gibt den Index eines Wertes zurück. Rückgabewert -1, falls Wert nicht in der Liste (Tipp: kann bereits implementierte Methode get_index_of_element nutzen) |
| +remove_element_at_index(index:int): boolean | True, falls Index existiert und die Liste geändert wurde, sonst False |
| +remove_element(element:object):boolean | True, wenn Element in Liste und gelöscht wurde (Tipp: kann bereits implementierte Methode get_index_of_element nutzen) |
| Zusatz: +sort():void | Selbsterklärend |
Implementiert die Methoden. Hier der bisherige Code mit Testaufrufen für die neuen Methoden: 18_linkedlist.py
Hinweis: Die Testaufrufe sind bereits unten implementiert. Es ist also erstmal normal, wenn Fehler angezeigt werden. (Stichwort: Testgetriebene Entwicklung). Eure Aufgabe ist es, die Fehler zu eliminieren.
Lösung: Lösung.py
¶ Datenstruktur Graph
Graph dient als mathematisches Modell zur Darstellung von Netzwerken.
Baum und Liste sind spezielle Formen der Datenstruktur Graph.
¶ Einsatz:
- Verbindungsnetzwerke (Flugverbindungen, Bahnnetzen, Autobahnnetzen)
- Verweisen (Literaturverweise, Wikipedia)
- technischen Modellen (Computergrafik, Platinen-Layout)
¶ Grundbegriffe:
- Jeder Eckpunkt eines Graphen heißt Knoten. Die Menge aller Knoten wird oft mit V (vertex) bezeichnet
- Jede direkte Verbindung zweier Knoten heißt Kante. Die Menge aller Kanten wird oft mit E (edge) bezeichnet
- Die Gesamtheit aller Knoten und Kanten heißt Graph. Der Graph wird oft mit G bezeichne
- Die Anzahl aller an einen Knoten angrenzenden Kanten heißt Grad des Knotens. Knoten D hat den Grad 3.

¶ Eigenschaften:
Ein Graph kann gerichtet/ungerichtet gewichtet/ungewichtet sein.

Die Datenstruktur Graph kann von Computern auf verschieden Arten gespeichert/repräsentiert werden.
Informiert euch dazu in folgenden Quelle. Beachtet die folgenden Kapitel: https://inf-schule.de/algorithmen/standardalgorithmen/graphen/implementierung/station_repraesentation
Ein Weg gibt eine Abfolge von Knoten von Startknoten zu einem Zielknoten an. Dabei wird kein Knoten mehrfach durchlaufen.
https://informatik-bg.de/unterrichtsmaterial/80-graphen/_Infomaterial-Graphen.pdf
¶ Algorithmen auf Graphen
Wie oben gesehen, gibt es viele Einsatzmöglichkeiten für Graphen. Ein typischer ist die Repräsentation von Orten den deren Verbindungen, also zum Beispiel Städten und Straßen auf einer Landkarte.
Es existieren verschiedene Algorithmen, um die kürzesten Wege zu berechnen.
Aufgabe
Informiert euch in folgender Quelle über den Dijkstra-Algorithmus und haltet seine Schritte stichpunkthaft fest.
https://www.youtube.com/watch?v=KiOso3VE-vI
https://www.youtube.com/watch?v=L5uuj2F61pc
Alles klar? Dann beweist es !
Aufgabe
Findet die kürzesten Wege ausgehend von Knoten A auf folgendem Arbeitsblatt
¶ Das Königsberger Brückenproblem
Königsberg wird durch den Pregel und seine beiden Inseln geteilt. Die beiden Stadthälften waren durch je drei Brücken mit den Inseln verbunden, die untereinander durch eine weitere Brücke verbunden waren.
Das Königsberger Brückenproblem bezeichnet die Frage, ob man alle 7 Brücken, welche das geteilte Königsberg verbinden mit einem Weg überqueren kann und falls ja, ein Rundweg möglich ist, bei welchen man an seinem Startpunkt wieder ankommen würde.


¶ Euler Kreis
Ein Eulerkreis ist ein geschlossener Pfad in einem Graphen, der jede Kante genau einmal durchläuft und am Ausgangspunkt endet.
Leonhard Euler bewies, dass ein zusammenhängender Graph ein Eulerkreis ist, wenn jeder Knoten eine gerade Anzahl von Kanten (also einen geraden Grad) hat. Dies war Teil seiner Lösung zum Königsberger Brückenproblem.
¶ Euler Weg
Ein Eulerweg ist wie der Eulerkreis ein geschlossener Pfad in einem Graphen, der jede Kante genau einmal durchläuft. Jedoch muss ein Eulerweg nicht den selben Start/Endpunkt haben.
Die vorstellung ist wie in der Realität:
ein Kreis ist eine Runde, als selber Start- und Endpunkt, ein Weg jedoch muss nicht zwangsläufig dort enden wo er anfing.
¶ Allgemeine: Wann gibt es einen Euler Weg / Kreis
- Eulerkreis: zusammenhängender Graph mit einer geraden Anzahl von Kanten
- Eulerweg: zusammenhängender Graph mit max. 2 ungeraden Kanten
¶ Datenstruktur Baum
...ist eine dynamische Datenstruktur, in dem Werte hierarchisch gespeichert werden.
Die Wurzel (englisch root) ist eine einzelner Knoten (englisch node), der keine Vorfahren hat.
Die Blätter sind die letzten Knoten im Baum, sie haben also keine Nachfolger.
Zusätzlich gibt es innere Knoten, die Vorgänger (auch Elternknoten) und Nachfolger (auch Kindsknoten) haben.
Ein Baum ist ein zusammenhängender & kreisfreier Graph.

¶ Binärbaum
besteht aus Wurzel und endlicher Anzahl an Knoten
jeder Knoten hat 0 bis 2 Zeiger auf weiteren Knoten --> Kinder des Knotens;
jeder hat genau einen Vater (außer Wurzel);
Regel: das rechte Kind ist größer als der Vater, das linke Kind kleiner
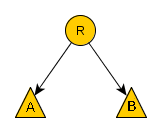
¶ AVL / höhe balancierter Baum
- Ein Baum ist höhenbalanciert, wenn die Höhe zweier beliebiger Blätter sich um nicht mehr als 1 unterscheidet.
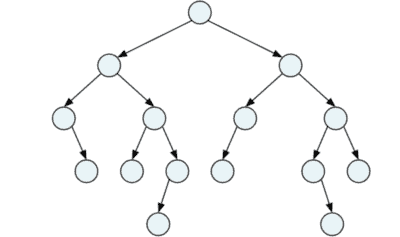
¶ Einfügen / Löschen / Suchen von Knoten
Einfügen:
- Beginn bei Wurzel
- zu einfügendes Element mit aktuellem Knoten vergleichen
- wenn kleiner links; sonst rechts
- ist kein Konten vorhanden einfügen, sonst wiederhole 2 mit aktuellem Knoten (rekursiver Aufruf)
hier klicken für genauere Anleitung!
Löschen:
- zu löschenden Knoten suchen
- wenn gefunden, dann löschen
- Fall keine Kinder: löschen
- Fall 1 Kind: ToDo
- Fall 2 Kinder: ToDo
hier klicken für genauere Anleitung!
Suchen:
- Beginn bei Wurzel
- zu suchendes Element mit aktuellen Knoten vergleichen
- wenn ==: gefunden
- wenn <: wiederhole 2. mit linkem Knoten
- sonst: wiederhole 2. mit rechem Knoten
¶ Implementierung Binärbaum
Implementieren Sie folgendes Klassendiagramm für den Binärbaum.
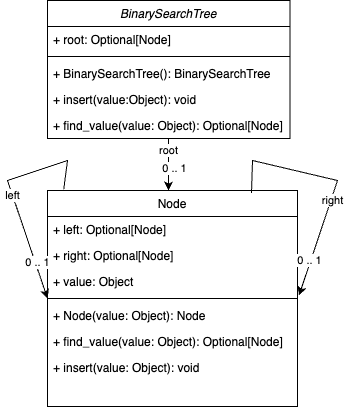
¶ Traversierung von Bäumen
frz. traverser, eng. to traverse ‚etwas durchschreiten‘, ‚überqueren‘
Traversierung ist […] der Name für Verfahren, die eine Route bestimmen, bei der jeder Knoten und jede Kante eines Graphen genau einmal besucht wird.
Für die Traversierung existierende verschiedene Möglichkeiten
Tiefensuche (Depth-First Search) folgt einem Pfad so tief wie möglich, bevor sie zurückgeht und andere Pfade untersucht.
Arten
- Pre-Order (Node, links, rechts)
- Post-Order (links, rechts, Node)
- In-Order (links, Node, rechts)
Breitensuche (auch Level-Order-Traversal): es werden die Knoten ausgehend von der Wurzel Ebene für Ebene, von links nach rechts, besucht.
Für die Implementierung benötigen wir eine Warteschlange, in die wir zunächst den Wurzelknoten einfügen und dann wiederholt
- das erste Element entfernen
- es besuchen und
- seine Kinder der Warteschlange hinzufügen - bis die Warteschlange wieder leer ist.
Gegeben ist folgender Baum. Geben Sie die Reihenfolge der Knoten in Pre-Order, Post-Order, In-Order un Level-Order an.
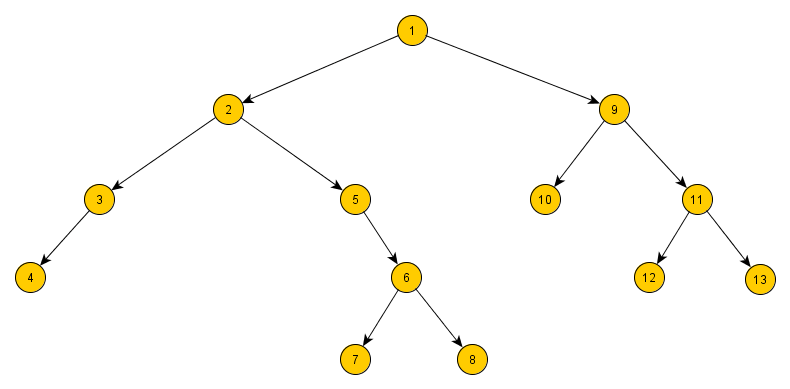
Ergänzen Sie das UML-Digramm des BinaryTrees um folgende Methoden und implementieren Sie diese.
- pre_order_place
- post_order_place
- in_order_place
- level_order_place (Breitensuche)
Lösung
class Node(object):
def __init__(self, value):
self.left = None
self.right = None
self.value = value
def find_node(self, value):
# sucht die Node für einen Wert value
# wenn value kleiner als eigener Wert -> links weitersuchen
if value < self.value:
if self.left is None:
# nicht gefunden
return None
# rekursiver Aufruf
return self.left.find_node(value)
# wenn value größer als eigener Wert -> rechts weitersuchen
elif value > self.value:
if self.right is None:
# nicht gefunden
return None
# rekursiver Aufruf
return self.right.find_node(value)
else:
# gefunden
return self
def insert(self, value):
if self.value < value:
if self.right == None:
self.right = Node(value)
else:
self.right.insert(value)
else:
if self.left == None:
self.left = Node(value)
else:
self.left.insert(value)
def in_order_place(self):
if self.left != None:
self.left.in_order_place()
print(self.value, end=" ")
if self.right != None:
self.right.in_order_place()
def pre_order_place(self):
print(self.value, end=" ")
if self.left != None:
self.left.pre_order_place()
if self.right != None:
self.right.pre_order_place()
def post_order_place(self):
if self.left != None:
self.left.post_order_place()
if self.right != None:
self.right.post_order_place()
print(self.value, end=" ")
class BinarySearchTree(object):
def __init__(self, root = None):
self.root = root
def insert(self, value):
if self.root is None:
self.root = Node(value)
else:
self.root.insert(value)
def find_node(self, value):
if self.root == None:
return
else:
return self.root.find_node(value)
def in_order_place(self):
if self.root == None:
return
else:
self.root.in_order_place()
def pre_order_place(self):
if self.root == None:
return
else:
self.root.pre_order_place()
def post_order_place(self):
if self.root == None:
return
else:
self.root.post_order_place()
def level_order_place(self):
q = []
q.append(self.root)
while q != []:
node = q.pop(-1)
if node != None:
print(node.value, end=" ")
q.append(node.left)
q.append(node.right)
if __name__ == "__main__":
nodeList = [9, 6, 11, 4, 8, 10, 13, 2, 5, 7]
# Baum Konstruktion
baum = BinarySearchTree()
for nd in nodeList:
baum.insert(nd)
# Baum Ausgaben
print("------Baum geordnet ausgeben ---------")
baum.in_order_place()
print()
baum.pre_order_place()
print()
baum.post_order_place()
print()
baum.level_order_place()
assert baum.find_node(11) != None, "Fehler: Baum enthält nicht Node 11"
assert baum.find_node(99) == None, "Fehler: Baum enthält Node 99"
¶ Breitensuche
Zum besseren Verständnis der Breitensuche, der Algorithmus in als Programmablaufplan.

¶ Datenstruktur Stack und Queue (Stapel und Schlange)
Stack und Queue sind lineare Datenstrukturen.
Ein Stack folgt entweder dem FILO oder LIFO Prinzip. Eine Queue folgt dem FIFO Prinzip.
- FILO (First-In Last-Out): Das Element, das der Datenstruktur zuerst hinzugefügt wurde, wird als Letztes wieder entfernt.
- LIFO (Last-In First-Out): Das Element, das der Datenstruktur als letztes hinzugefügt wurde, wird als erstes wieder entfernt
- FIFO (First-In First-Out): Das Element, das der Datenstruktur zu erst hinzugefügt wird, wird auch als erstes wieder entfernt.
Folgende Tabelle zeigt typische Methoden eines Stacks.
| Stack | |
|---|---|
| + empty(): boolean | Gibt zurück, ob der Stack leer ist – Zeitkomplexität: O(1) |
| + size(): int | Gibt die Größe des Stacks zurück – Zeitkomplexität: O(1) |
| + top(): Object (auch peek genannt) | Gibt eine Referenz zum obersten Element des Stacks wieder – Zeitkomplexität: O(1) |
| + push(element: Object): void | Fügt das Element ‘a’ auf die "Spitze" des Stapels ein – Zeitkomplexität: O(1) |
| + pop(): void | Löscht das oberste Element des Stapels – Zeitkomplexität: O(1) |
Folgende Tabelle zeigt typische Methoden einer Queue.
| Queue | |
|---|---|
| + enqueue(element: Object): void | Fügt das Element an der hintersten Stelle der Queue an - Zeitkomplexität: O(1) |
| + dequeue(): Object | Entfernt das Element an vorderster Stelle der Queue - Zeitkomplexität: O(1) |
| + front(): Object | Gibt das erste Element zurück - Zeitkomplexität: O(1) |
| + rear(): Object | Gibt das letzte Element zurück - Zeitkomplexität: O(1) |
Beispiel Queue:
- Schlange im Supermarkt: die Person, die vorne in der Schlange steht, wird zuerst bedient (FIFO)
- Ein Server arbeitet Anfragen in der Reihenfolge ab, in der sie gestellt wurden.
Aufgabe 1: https://inf-schule.de/algorithmen/standardalgorithmen/stapel/exkurs_klassestapel
Aufgabe 2: https://inf-schule.de/algorithmen/standardalgorithmen/schlangen/exkurs_klasseschlange
Lösung
Lösung mit typischen Namen
Aufgabe 3: https://inf-schule.de/algorithmen/standardalgorithmen/stapel/anwendung_rechenterme
¶ Modularisierung
Ein Gesamtsystem wird aus
wiederverwendbaren Einzelbausteinen („Module“) zusammengesetzt.
Vorteile
- Strukturierung von Programmen
- Vermeidung von Codeduplizierung
- Erhöhung der Wiederverwendbarkeit
Funktionen und Prozeduren sind Verarbeitungseinheiten, die übergebene Daten (Parameter) verarbeitet
| Funktion | Prozedur | |
|---|---|---|
| Rückgabewert | ja | nein |
| Seiteneffekt | evtl.; bei Paradigma Funktionaler Prigrammierung nein | idR. ja |
| Beispiel | input, sorted([1,5,3]]) | print, [1,5,3].sort() |
¶ Parameter
Begriffe
- „Parameter“ bei Definition
- „Argumente“ bei Aufruf
Beispiel
- Parameter: gewicht und groesse
- Argumente für die Parameter: 70 und 1.75
def berechne_bmi(gewicht: float, groesse: float) -> float:
"""
Berechnet den Body-Mass-Index (BMI).
:param gewicht: Gewicht in Kilogramm
:param groesse: Größe in Metern
:return: BMI-Wert
"""
if groesse <= 0:
raise ValueError("Die Größe muss größer als 0 sein.")
bmi = gewicht / (groesse ** 2)
return round(bmi, 2)
# Beispiel
bmi = berechne_bmi(70, 1.75)
print(f"Der berechnete BMI ist: {bmi}")
Gibt für berechne_bmi begründet an, ob es sich um eine Funktion oder Prozedur handelt.
¶ Wertübergabe (call by value)
-
jedes Argument stellt einen Wert dar, der ausgewertet wird
-
Werte von übergebenen Parametern können nicht geändert werden
-
bei primitiven Datentypen
¶ Referenzübergabe(call by reference)
-
Referenzen (Speicheradressen) werden übergeben
-
Änderungen wirken sich auch auf aufrufenden Teil des Programmes aus
-
bei komplexen Datentypen
¶ Beispiel
def call_by_value(x):
"""Diese Funktion zeigt Call by Value mit einem unveränderlichen Typ (Integer)."""
print(f"Vor Änderung in Funktion: x = {x}")
x = 10 # Änderung innerhalb der Funktion
print(f"Nach Änderung in Funktion: x = {x}")
def call_by_reference(lst):
"""Diese Funktion zeigt Call by Reference mit einer veränderlichen Liste."""
print(f"Vor Änderung in Funktion: lst = {lst}")
lst.append(4) # Änderung innerhalb der Funktion
print(f"Nach Änderung in Funktion: lst = {lst}")
# Call by Value (unveränderlicher Typ)
a = 5
print(f"Vor Funktionsaufruf: a = {a}")
call_by_value(a)
print(f"Nach Funktionsaufruf: a = {a}\n") # 'a' bleibt unverändert
# Call by Reference (veränderlicher Typ)
b = [1, 2, 3]
print(f"Vor Funktionsaufruf: b = {b}")
call_by_reference(b)
print(f"Nach Funktionsaufruf: b = {b}") # 'b' wurde verändert