¶ Binär- und Hexadezimalsystem
TimeToPlayAGame
https://learningcontent.cisco.com/games/binary/index.html
Zusammenfassung: https://studyflix.de/informatik/zahlensysteme-402
| Begriff | Bedeutung |
|---|---|
| Zahlensystem | Zahlensysteme werden zur Darstellung von Zahlen verwendet. |
| Ziffer | Ziffern sind einstellig |
| Polyadisch | ein polyadisches Zahlensystem ist ein Zahlensystem, dessen Zahlzeichen aus Ziffern besteht, deren jeweiliger Beitrag zum Gesamtwert der Zahl von ihrer Position innerhalb des Zahlzeichens abhängt |
| Dezimal | auf der Grundzahl 10 beruhend - auf die Basis 10 bezogen |
| Binärsystem | Zahlensystem, das zur Darstellung von Zahlen nur zwei verschiedene Ziffern benutzt |
| Hexadezimal | werden Zahlen in einem Stellenwertsystem zur Basis 16 dargestellt. „Hexadezimal“ |
¶ Umwandlung aus beliebigen Zahlensystem in Dezimalsystem
Formel aus dem Video:
ND = dn * Rn + ... + d1 * R1 + d0 * R0
- N = Number
- d = digit
- n = index
- R = Radix (Basis)
Übungen Umwandlung Zahlsystem in Dezimalsystem
- 101102 =
- 56922 =
- 25368 =
- 12023 =
- https://de.serlo.org/informatik/184941/aufgaben-zu-zahlensystemen
Umwandlung in Python
zahlenumwandlung.py
¶ Umwandlung von Dezimalsystem in beliebiges Zahlensystem
Übungen Umwandlung Dezimalsystem in anderes Zahlensystem
Algorithmus
- Teile durch Basis und Notiere Ergebnis und Rest
- Wiederhole vorherigen Schritt solange Ergebnis != 0
- Ergebnis rückwärts gelesen ist neue Zahl
- https://de.serlo.org/informatik/184941/aufgaben-zu-zahlensystemen (Aufgabenkomplex 4)
¶ rechnerinterne Zahlenformate
- Einerkomplement
- Zweierkomplement
- Festkommazahlen
¶ Komplementierungen
Komplementierungen sind dazu da, um Zahlen im binären System auch negativ darstellen zu können. Man kann die Komplementierungen grundsätzlich in zwei Methoden unterscheiden: Einer- und Zweierkomplement. Es ist für den Computer wichtig zu wissen, in welcher Methode gerade gearbeitet wird. Zudem wird die vorderste Stelle der Binärzahl für das Vorzeichen reserviert. Wenn also eine 1 vorne steht, steht diese für das Vorzeichen Minus.
¶ Einerkomplement
Im Einerkomplement werden, um negative Zahlen darzustellen, die normalen Binärzahlen einfach invertiert (umgekehrt) werden, damit die negative Zahl einer bestimmmten Zahl entsteht.
Bsp.: Wir wollen nun die zahl 6 in die -6 umwandeln. Wir bleiben dafür im 4bit-System.
6 = 0110
nun invertieren wir die Binärzahl
0110 = 1001
und schon haben wir unsere negative 6 (-6) im Einerkomplement dargestellt.
¶ Zweierkomplement
Im Zweierkomplement werden, um negative Zahlen darzustellen, die normalen Binärzahlen invertiert (umgekehrt) und dann mit der Binären Eins addiert.
Bsp.: Wir wollen nun die zahl -6 im 4bit-System darstellen
6 = 0110
nun inventieren wir die 6
-> 1001
als nächstes addieren wir die Binäre 1 (0001)
_1001
+00011
-6=1010
Zusammenfassung Zweierkomplement: https://www.youtube.com/watch?v=utqzSGXd4X4
¶ Zeichenkodierung
Koodierungen sind "Zuordnung von Bitkombinationen zu den Zeichen eines Alphabets/Zeichenvorrates." (Quelle: https://de.wiktionary.org/wiki/Kodierung).
Die Buchstaben dieses Wikis müssen zum Beispiel in Bitkombination/Zahlen umgewandelt werden, um auf der Festplatte gespeichert zu werden.
Beispiele für Zeichenkodierung sind ASCII oder UTF-8.
Folgende Tabelle zeigt, einen Ausschnitt der ASCII Kodierung.
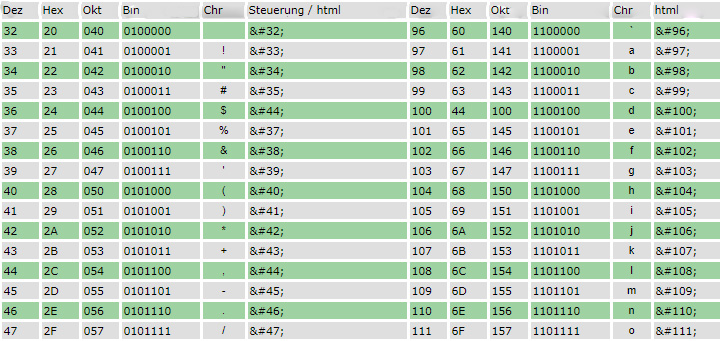
Quelle: https://blog.zeta-producer.com/ascii-code/ascii-tabelle-2/