¶ Kryptographie und Kryptoanalyse
Kryptographie bezeichnet die Wissenschaft von der Verschlüsselung von Daten.
Kryptoanalyse bezeichnet die Wissenschaft des Entschlüsselns von Geheimtexten, ohne den geheimen Schlüssel zu kennen.
¶ Anforderungen an die Informationssicherheit
- Vertraulichkeit: Schutz vor unbefugtem Zugriff auf Informationen.
- Integrität: Sicherstellung, dass Daten vollständig und unverändert sind
- Authentizität: Nachweis, dass eine Information einem eindeutigen Absender zugeordnet werden kann
- Verbindlichkeit: Nachweisbarkeit von Handlungen, sodass diese nicht abgestritten werden können.
- Verfügbarkeit: Gewährleistung, dass Informationen und Systeme jederzeit nutzbar sind.
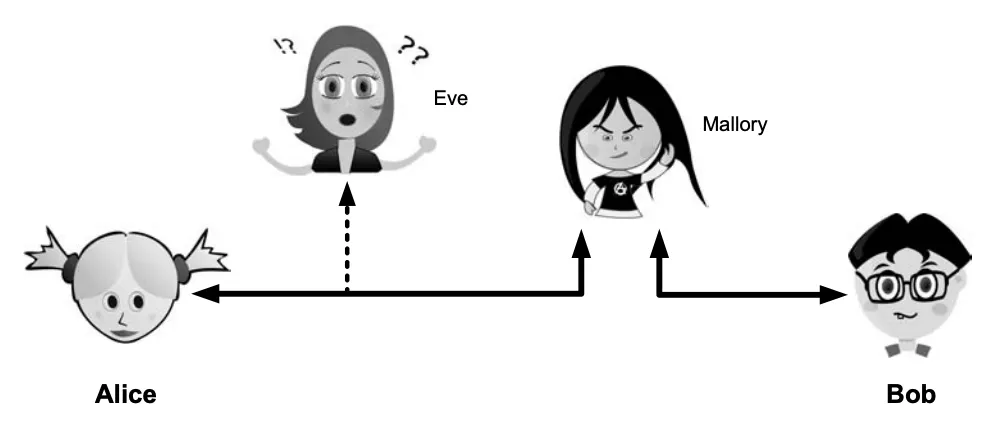
¶ Kommunikationspartner
| Name | Rolle |
|---|---|
| Alice + Bob | Kommunikationspartner |
| Eve | abhören der Kommunikation (von eavesdropping) |
| Mallory | bösartiger Eingriff in Kommunikation |
| Trend | vertrauenswürdige dritte Instanz (von trusted entity) |
¶ Gewährleistung der Vertraulichkeit
¶ symmetrische vs. asymmetrisch Verschlüsselungsverfahren
| Eigenschaft | symmetrische | asymmetrisch |
|---|---|---|
| Schlüssel | ein Schlüssel | ein Schlüsselpaar (public key + private key) |
| Geschwindigkeit | sehr schnell | deutlich langsamer |
| Schlüsselverteilung | Übergabe vor Ort / in Person -> Unsicher | Nutzung von Schlüsselpaaren |
| Schlüsselanzahl bei n Teilnehmern | n(n-1)/2 | 2n |
| Historische Algorithmen | Skytale, Caeser-Chiffre, Vigenère-Chiffre | Diffie-Hellman-Verfahren, RSA-Verfahren |
| Moderne Algorithmen | AES, Blowfish, Twofish | RSA, ECC |
| Einsatzgebiet | schnelle Speicherung großer Datenmengen & Festplatten | Websites, Emails, Kryptowährung |
Hybride Verschlüsselung kombiniert die Vorteiler von sym. und asym. Verschlüsselung. Symmetrische Schlüssel werden asymmetrisch ausgetauscht.
¶ Symmetrische Verschlüsselungen
Ein symmetrischen Kryptosystem ist ein Kryptosystem, bei welchem beide Teilnehmer einen gemeinsamen geheimen Schlüssel benötigen.
Quelle: https://de.wikipedia.org/wiki/Symmetrisches_Kryptosystem
¶ Historische Verfahren

https://youtu.be/QhwcD4XHHJ8?si=zJnmA2BMruDB0qMb
¶ Grundbegriffe
-
Klartext / Nachricht / m (message)
-
Geheimtext / Ciphertext / c
-
Schlüssel / Key / k
-
Klartextalphabet
-
Geheimtextalphabet
¶ Symmetrische Verschlüsselung
- Verschlüsselungsfunktion / encrypt: e(m, k) = c
- Entschlüsselungsfunktion / decrypt: d(c, k) = m
¶ Kerckhoff’s Prinzip
Die Sicherheit eines Kryptosystems darf nicht von der Geheimhaltung des Algorithmus abhängen, sondern nur von der Geheimhaltung des Schlüssel.
Annahmen:
- Genutzter Algorithmus ist allen bekannt
- Schlüssel allein ist geheim
- Verfahren muss schnell und einfach anwendbar sein
- Dem Angreifer ist alles bekannt bis auf dem Geheimschlüssel, zudem besitzt er hohe Rechenleistung
- Sicherheit darf nicht von Geheimhaltung oder Schutz bestimmter Geräte abhängen
¶ Verschiebeverfahren am Beispiel Caesar
-
Klartextalphabet = Geheimtextalphabet = [A, B, C, ..., X, Y, Z ]
-
Schlüssel k = die Verschiebung, häufig dargestellt als Zeichen des Alphabets
Bsp: A verschiebt um 0 Stellen, B um 1 Stelle, ..., Z um 25 Stellen. -
Anzahl der Schlüssel = länge des Alphabets = 26

¶ Kryptoanalyse bei Caesar
- Bruteforce: Ausprobieren aller Schlüssel. Einfach, da wenig Schlüssel. Höchstens bei unendlich großem Alphabeten sicher, die es aber nicht gibt.
- Häufigkeitsanalyse: Zählen der Buchstaben. Rückschluss auf häufigsten Buchstaben der Klartextsprache. Möglich, da Caesar monoalphabetisch ist.
Definition: Monoalphabetisch
Jedes Zeichen wird durch ein festgelegtes anderes Zeichen ersetzt.
Zum Verschlüsseln eines Textes wird nur ein Alphabet verwendet (mono).
Implementierung von Caesar: Caesar Implementierung
Alternative Implementierung mit Erklärung: https://inf-schule.de/imperative-programmierung/python/projekte/modularisierung/verschluesselung/zuordnungstabelle
¶ Ersetzungsverfahren (auch Substitutionschiffre)
Jedem Buchstaben wird ein anderer Buchstabe des Alphabets zugeordnet. Die Zuordnungstabelle kann dabei willkürlich gewählt werden - sie muss nur eindeutig sein.
Beispiel:
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z = Klartextalphabet
G K X C S L Z U A H W D B M T Y E N J V P O I R F Q = Geheimtextalphabet
¶ Kryptoanalyse beim Ersetzungsverfahren
- Bruteforce: praktisch nicht möglich, das hohe Anzahl an Schlüsseln: Alphabetlänge!. Bei 26 Buchstaben 26! = 4.0329146 * 1026
- Häufigkeitsanalyse: einfach möglich, da monoalphabetisch
¶ Vigenère
Wie Caesar mit längerem Schlüssel, daher polyalphabetisch.
Die Vigenère Chiffre kombiniert 26 monoalphabetische Verschlüsselungen.

¶ Kryptoanalyse bei Viginiere
Kasiski veröffentlichte 1863 einen Test zur Bestimmung der Schlüssellänge.
Der Geheimtext wird dazu nach sich wiederholenden N-Grammen durchsucht.
Bigramme = 2 Zeichen
Trigramme = 3 Zeichen
....
Die vermutete Schlüssellänge ist, bis auf Ausreißer, ein Teiler der Abstände zwischen den N-Grammen.
Ist die Schlüssellänge bekannt, wird der Geheimtext in Mengen aufgeteilt.
Beispiel: Schlüssellänge 3: Der Geheimtext wird in 3 Mengen aufgeteilt
- Jedes 3. Zeichen startend vom 1. Zeichen
- Jedes 3. Zeichen startend vom 2. Zeichen
- Jedes 3. Zeichen startend vom 3. Zeichen
Auf jeder dieser 3 Mengen kann die Häufigkeitsanalyse angewendet werden, da innerhalb der Menge monoalphabetisch verschlüsselt wurde.
Im Detail: https://inf-schule.de/kryptologie/historischechiffriersysteme/station_kryptoanalysevigenereverfahren
¶ One-Time-Pad (OTP)
Ist ein Verschlüsselungsverfahren, das bei korrekter Anwendung theoretisch unknackbar ist.
Anforderungen an Schlüssel:
- wirklich zufällig
- mindestens so lang ist wie die Nachricht
- nur ein einziges Mal verwendet wird (daher one-time)
- bleibt streng geheim
¶ Schlüsseltauschproblem
Das Schlüsseltauschproblem bezeichnet die Herausforderung, bei symmetrischen Verfahren einen geheimen Schlüssel sicher zwischen den Kommunikationspartnern auszutauschen.
¶ One-Way-Hash-Funktion, Block-Chain und digitale Signaturen
- link zur Slide: https://docs.google.com/presentation/d/12DMtTPZUa7ss_EqZtI2E8LYA4sqlGmN6cKUGwNeqh3Y/edit?usp=drive_link
- Die Unterseite zum One-Way Hash: One_Way_Hash
- Die Unterseite zur Block-Chain: Block_Chain
- Die Unterseite zu digitalen Signaturen: Digitale_Signaturen
¶ Asymmetrische Verschlüsselungen
Jede Kommunikationspartei besitzt ein Schlüsselpaar, das aus einem geheimen Teil (geheimer/privater Schlüssel) und einem nicht geheimen Teil (öffentlicher Schlüssel) besteht. > Der öffentliche Schlüssel ermöglicht es jedermann Daten für den Inhaber des dazugehörigen geheimen Schlüssels zu verschlüsseln. Die verschlüsselten Daten lassen sich nicht mit dem öffentlichen, sondern nur mit dem geheimen Schlüssel entschlüsseln.
Asymmetrische Systeme werden auch als Public-Key-Verfahren bezeichnet.
Quelle: https://informatik.mygymer.ch/ef2021/010.krypto/03.asymmetrische.html#prinzip
¶ Asymmetrische Verschlüsselung
- Verschlüsselungsfunktion / encrypt: e(m, kpublic) = c
- Entschlüsselungsfunktion / decrypt: d(c, kprivate) = m
Die Berechnung des Schlüsselpaar verwendet eine Falltürfunktion. Die Berechnung ist leicht in eine Richtung aber schwer in die andere.
"Grundsätzlich ist es möglich, aus dem privaten den öffentlichen Schlüssel – und umgekehrt – zu berechnen. Es ist nur sehr aufwändig. Es wäre durchaus möglich, dass man eines Tages einen Algorithmus entdeckt, mit dem man schnell und in kurzer Zeit grosse Zahlen faktorisieren kann. Man vermutet weiterhin, dass man alle Einwegfunktionen mit ausreichend Rechen- und Zeitaufwand umkehren kann – auch 300-stellige Schlüssel. Gelungen ist es bis jetzt aber noch nicht. RSA ist also nur so lange sicher, wie die (momentane) Unfähigkeit, grosse Zahlen in vernünftiger Zeit zu faktorisieren, bestehen bleibt."
Quelle: https://informatik.mygymer.ch/ef2021/010.krypto/03.asymmetrische.html#vor-und-nachteile
¶ Diffie-Hellman Schlüsseltausch
Diffie-Hellman Schlüsseltausch ermöglicht es zwei Parteien, über ein unsicheres Netz einen gemeinsamen geheimen Schlüssel zu erzeugen, ohne ihn direkt zu übertragen.
¶ Ablauf:
- Alice und Bob wählen öffentlich eine Primzahl p und eine Basis g
- Alice wählt eine geheime Zahl a und berechnet A = g^a mod p
Bob wählt eine geheime Zahl b und berechnet B = g^b mod p - Sie tauschen A und B aus
- Alice berechnet K = B^a mod p
Bob berechnet K = A^b mod p - Beide besitzen nun denselben geheimen Schlüssel K, da gilt:
(gb)a mod p = (ga)b mod p
Der Schlüssel selbst wird nie übertragen. Sicherheit beruht darauf, dass das diskrete Logarithmusproblem sehr schwer zu lösen ist.
¶ RSA
- Die Unterseite zum RSA-Verfahren: RSA
- Ein Tool für die Schlüsselberechnung: https://tools.justus-d.de/rsa/
¶ Aufgabe
Stellt zu zweit ein asymmetrisches Kryptosystem nach:
Generiert jeweils einen asymmetrischen Schlüssel
Tausch den öffentlichen Teil
Generiert eine Nachricht, verschlüsselt und verschickt sie.
Entschlüsselt die Nachricht.
Identisch für Signatur (einigt euch auf eine Hash-Funktion)Ihr könnt folgendes Tool verwenden: https://www.devglan.com/online-tools/rsa-encryption-decryption
¶ Kryptoanalyse
- Brute-Force-Methode
- Häufigkeitsanalyse
- Social Engineering
¶ Datensicherung
- Komplettsicherung
- differentielle Sicherung
- inkrementelle Sicherung
- RAID (redundant array of inexpensive disks)
¶ Zusammenfassung und Einblick Quantencomputer
¶ Datenschutz
Im folgenden geht es personenbezogene Daten.
Das bedeutet: Wenn Daten direkt oder indirekt einer bestimmten Person zugeordnet werden können, gelten sie als personenbezogen.
¶ Beispiel für personenbezogene Daten
Die Unterseite zu den Beispielen: personenbezogene_Daten
¶ Prinzipchen des Datenschutzes
- Datensparsamkeit: bei der Verarbeitung personenbezogener Daten so wenige Daten wie möglich erhoben, gespeichert und genutzt werden sollen.
- Erforderlichkeit
- Zweckbindung
- Recht auf informationelle Selbstbestimmung: jede Person grundsätzlich selbst darüber entscheiden darf, welche persönlichen Daten sie preisgibt und wie diese verwendet werden dürfen.
¶ Rechtliches
¶ Datenschutz-Grundverordnung (DSGVO)
¶ Ziele
- Schutz personenbezogener Daten von natürlichen Personen
- Freier Datenverkehr innerhalb des EU-Binnenmarkts
- Einheitliche Regeln in allen Mitgliedsstaaten
- Rechtmäßigkeit, Verarbeitung nach Treu und Glauben, Transparenz
- Zweckbindung – Daten dürfen nur für festgelegte Zwecke genutzt werden
- Datenminimierung – nur so viele Daten, wie erforderlich
- Richtigkeit – Daten müssen korrekt und aktuell sein
- Speicherbegrenzung – Löschung, wenn nicht mehr nötig
- Integrität und Vertraulichkeit – Sicherheit der Daten
- Rechenschaftspflicht – Verantwortliche müssen die Einhaltung nachweisen können
¶ Rechte der Betroffenen
- Auskunftsrecht (Art. 15) → Welche Daten werden verarbeitet?- Recht auf Berichtigung (Art. 16)
- Recht auf Löschung („Recht auf Vergessenwerden“) (Art. 17)
- Recht auf Einschränkung der Verarbeitung (Art. 18)
- Recht auf Datenübertragbarkeit (Art. 20)
- Widerspruchsrecht (Art. 21)
- Recht, nicht ausschließlich automatisierten Entscheidungen unterworfen zu sein (Art. 22)
Grundprinzipien
